Unveiling the Power of Variational Autoencoders (VAEs) in Generative AI

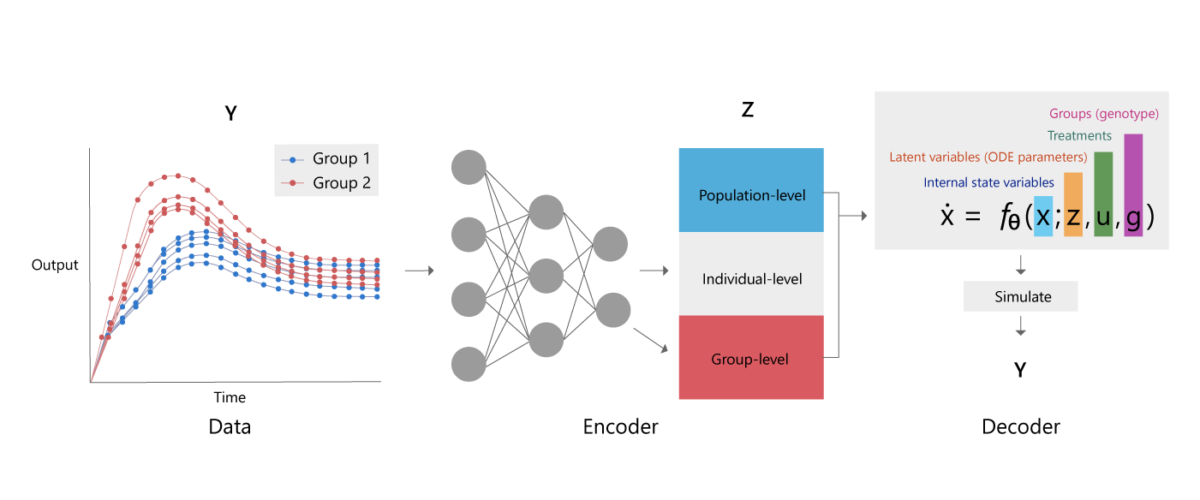
Variational Autoencoders (VAEs) are a powerful and popular class of generative models in the field of machine learning. Introduced by Diederik P. Kingma and Max Welling in 2013, VAEs have gained significant attention for their ability to learn rich latent representations of data and generate new samples that resemble the training data. VAEs combine the principles of autoencoders and probabilistic modeling to enable efficient and flexible generation of complex data.

At the core of VAEs lies the idea of learning a low-dimensional representation, or latent space, that captures the essential features and variations in the data. VAEs consist of two components: an encoder and a decoder. The encoder maps the input data to a latent space, typically represented by a mean and variance, while the decoder reconstructs the input data from samples in the latent space.

What sets VAEs apart from traditional autoencoders is their probabilistic formulation. VAEs model the latent space as a probability distribution, typically a Gaussian distribution, allowing for the sampling of new data points from this distribution. This stochasticity introduces a regularization mechanism that encourages the learning of a smooth and structured latent space, enabling meaningful generation of new data samples.

The training process of VAEs involves maximizing the evidence lower bound (ELBO) objective, which consists of two terms: the reconstruction loss, which measures the similarity between the reconstructed data and the original data, and the regularization term, which encourages the latent space to adhere to the desired distribution. By optimizing this objective, VAEs learn to encode the input data into a latent representation and generate new samples by sampling from the latent space.

The flexibility and generative capabilities of VAEs have led to their widespread applications in various domains. They have been successfully employed in image generation, data synthesis, dimensionality reduction, anomaly detection, and semi-supervised learning, among others. VAEs offer a powerful framework for learning rich representations and exploring the underlying structure of complex data.

In the following sections, we will delve deeper into the working principles of VAEs, explore their applications in different fields, discuss training and evaluation considerations, and examine the challenges and future directions of this exciting area of research. Join us on this journey as we unravel the fascinating world of Variational Autoencoders (VAEs) and their transformative potential.

Explain the Power of Variational Autoencoders (VAEs) in Generative AI

Variational Autoencoders (VAEs) possess significant power in the field of generative AI. Their unique formulation and capabilities contribute to their effectiveness in generating new data samples and learning meaningful latent representations. Let’s explore the power of VAEs in generative AI:

• Latent Space Representation: VAEs learn a compressed and structured latent space representation of the input data. This latent space captures the underlying variations and features present in the data. By exploring this latent space, VAEs enable efficient and meaningful generation of new data samples. The latent space provides a continuous and interpretable representation, allowing for smooth interpolation and controlled synthesis of data points.
• Probabilistic Framework: VAEs employ a probabilistic framework to model the latent space. This probabilistic formulation allows for sampling from the latent space, facilitating the generation of diverse and novel data samples. By modeling the latent space as a probability distribution, typically a Gaussian distribution, VAEs can generate data samples that possess desired characteristics or variations. This stochasticity enhances the flexibility and creativity of the generative process.
• Reconstruction Loss: VAEs utilize a reconstruction loss to guide the learning process. The reconstruction loss measures the similarity between the reconstructed data and the original input data. This loss encourages the VAE to learn to reconstruct the input data faithfully, ensuring that the generated samples resemble the training data. The reconstruction loss contributes to the ability of VAEs to generate realistic and high-quality data samples.
• Data Synthesis and Augmentation: VAEs offer the capability to generate new data samples that closely resemble the training data distribution. This has significant implications in data synthesis and augmentation tasks. VAEs can generate synthetic data points that can be used to augment training datasets, increasing their diversity and size. This data augmentation improves the generalization and robustness of machine learning models trained on limited data.
• Unsupervised and Semi-Supervised Learning: VAEs can be used for unsupervised learning tasks, where there is no labeled data available. By learning the latent representation of the data, VAEs can capture the underlying structure and variations in the data, enabling tasks such as clustering, dimensionality reduction, and anomaly detection. VAEs can also be extended to semi-supervised learning scenarios, where a small amount of labeled data is available. By leveraging the generative capabilities of VAEs, they can effectively utilize both labeled and unlabeled data to improve classification and prediction tasks.
• Transfer Learning and Representation Learning: VAEs facilitate transfer learning by allowing the transfer of learned knowledge from one dataset to another. The learned latent representation can be used as a feature extractor for downstream tasks, reducing the need for extensive training on new datasets. VAEs excel at representation learning, as the latent space captures meaningful and disentangled representations of the input data. This disentanglement enables the extraction of high-level semantic features, contributing to improved performance in various tasks.
• Interpretability and Explainability: The structured and continuous nature of the latent space in VAEs allows for interpretability and explainability of the generative process. Each dimension in the latent space can correspond to a specific attribute or feature of the data. By manipulating the values of individual dimensions, one can control and understand the impact on the generated data. This interpretability is valuable in applications where understanding the generative process is crucial.
• Creative Applications: VAEs have found applications in creative fields such as art, design, and music. Their generative capabilities enable the creation of novel and unique content. Artists and designers can explore the latent space to generate new images, styles, and compositions, providing a source of inspiration and pushing the boundaries of traditional approaches.

The power of Variational Autoencoders (VAEs) lies in their ability to learn meaningful latent representations, generate diverse and realistic data samples, and facilitate unsupervised and semi-supervised learning tasks. With their probabilistic formulation and flexible generative process, VAEs offer a versatile framework for generative AI, opening up new possibilities in various domains and driving innovation in the field.

Conclusion

Variational Autoencoders (VAEs) have proven to be a powerful tool in the field of generative AI. Through their unique formulation and capabilities, VAEs have demonstrated their prowess in generating new data samples and learning meaningful latent representations. The power of VAEs lies in their ability to model the latent space as a probability distribution, enabling efficient and controlled generation of diverse and realistic data samples.

By exploring the structured latent space, VAEs offer a compact representation that captures the underlying variations and features of the input data. This latent space serves as a foundation for generating new data points with desired characteristics and facilitating smooth interpolation between data samples.

The probabilistic framework of VAEs allows for the sampling of data points from the latent space, contributing to the flexibility and creativity of the generative process. The reconstruction loss employed by VAEs ensures that the generated samples resemble the training data, leading to the production of high-quality and realistic data samples.

Moreover, VAEs have applications beyond data generation. They excel in unsupervised and semi-supervised learning tasks, enabling tasks such as clustering, dimensionality reduction, and anomaly detection. VAEs also facilitate transfer learning and representation learning by extracting meaningful features from the learned latent space, reducing the need for extensive training on new datasets.

The interpretability and explainability of VAEs further enhance their utility. By manipulating individual dimensions of the latent space, one can understand and control the generative process, making VAEs valuable in domains where interpretability is crucial.

Additionally, VAEs find creative applications in art, design, and music, empowering artists and designers to explore new artistic directions and generate unique content.

As VAEs continue to evolve and researchers delve deeper into their capabilities, we can expect further advancements and applications in generative AI. VAEs offer a promising framework that combines the power of generative models, probabilistic modeling, and latent representations, paving the way for exciting developments in the field.

In conclusion, Variational Autoencoders (VAEs) have demonstrated their power and potential in generative AI by enabling efficient data generation, learning meaningful latent representations, and facilitating unsupervised and semi-supervised learning tasks. With their unique formulation and capabilities, VAEs contribute to advancements in diverse domains, driving innovation and creativity in the field of generative AI.